Lexical Analysis

这一章节我们来简单介绍下词法分析（Lexical Analysis）的基本逻辑和其中一些比较重要的概念。

一个例子

我们来把英语和编程语言进行类比。当我们在阅读一个英语句子时，我们首先会将其从左至右的进行单词划分并对词性进行判断，而在此过程中，我们需要根据一定的**知识（规则）**来帮助我们完成这个工作。对于编译器它也是如此。举例来说我们可以这样划分：

# English
We learned about lexical analysis today.

# <lexical_category, word_value>
<pron, "We">, <verb, "learned">, <adverb, "about">, <adjective, "lexical">, <noun, "analysis">, <adverb, "today">

# programming language
int a = 1;

# <token_class, token_value>
<keyword, "int">, <identifier, "a">, <operator, "=">, <integer, "1">, <operator, ";">

词法分析

简而言之，词法分析就是完成以下的两件事情：

  1. 从左到右阅读源程序，将源程序划分为一个个词素（每个词素都是字符串）。接着根据不同词素将其归为不同的语法单元（token）。

Token：记做一个二元组 <token_class, token_value>

token_class 的常见种类包括标识符（identifier）、关键词（keyword）、整数（integer）、空白（whitespace）。

token_value 就是我们的词素。

  1. 利用「向前看（lookahead）」操作帮助确定当前词素是否结束、下一个词素是否开始。

而对于词法分析器来说，要完成上述两个工作，离不开以下几个步骤：

1
  • 词法规则（Lexical Specification）：告诉我们什么样的词法是合法的。
  • 正则表达式（Regular Expressions）：一种描述词法规则的描述方式。用于描述定义的词法规则。
  • 非确定有穷状态机（Non-deterministic Finite Automata）：一种机器理解正则表达式的等价结构。
  • 确定有穷状态机（Deterministic Finite Automata）：一种机器理解正则表达式的等价结构（执行速度更快）。
  • 状态机的实现：需要借助表来帮助实现。

正则表达式

在我的理解来说，这个正则表达式和我们平常使用的、用于进行字符串匹配、特定语法字符串提取的那个正则表达式是相似的（或者说本质上就是一致的）。我们在平常的使用中也能感受到正则表达式能够很好的表达我们定义的词法规则。而程序在本质上都是由字符串构成的，因此正则表达式本质上也是在字符串上进行操作，这里就不详细介绍了，举例子来说明：

  • 关键字 if 通过单个字母 i 和 f 通过连接操作进行构建。
  • 任意长的数字可以表示为 [0-9]*（0-9可以代表从0到9的数字集合）;
  • 标识符可以表示为 [_a-zA-Z][_a-zA-Z0-9]*（a-z 和 A-Z 与 0-9 同理);

正则表达式仅仅是用来表述语言规则的一种形式，更方便与进行表述和理解。而机器想要理解正则表达式，我们就需要引入另一种等价的结构，也就是上图中的 NFA 和 DFA。

有穷自动机

介绍 NFA 和 DFA 之前，我们先来介绍一下他们名称中都有的 FA 代表的究竟是什么？ FA = Finite Automata 代表有穷自动机，也可以叫做（Finite State Machine，FSM），而一个有穷自动机往往都需要包含以下元素：

  1. 一个输入字符集 Σ\varSigma。
  2. 一个有穷的状态集合 SS。
  3. 一个起始状态 nn。
  4. 一个终止状态集合 ⊂\subset。
  5. 一系列状态转换 state⟶inputstatestate\stackrel{input}{\longrightarrow}state。

确定性的有穷自动机则是在上述的基础上满足更多的条件：

  • 对于每个状态而言，一个输入只能确定唯一的一个状态转换；
  • 没有 ϵ−moves\epsilon-moves；

相比较来说，非确定性的有穷自动机则是满足：

  • 对于每个状态而言，一个输入可以执行多个不同的状态转换；
  • 可有 ϵ−moves\epsilon-moves；
请注意!

ϵ−moves\epsilon-moves 是一种特殊的状态转换。它表示的是 state⟶ϵstatestate\stackrel{\epsilon}{\longrightarrow}state，也就是不需要接收输入字符的同时，就可以完成状态转换。
本质上来说，DFA 和 NFA 对于正则表达式的识别能力是完全相同的。但是 NFA 的优势在于状态空间更简单，DFA 则是执行速度更快。这会在后面进行讲解。

正则到 NFA

这里简单介绍下正则语言到 NFA 的过程，可能会涉及到一点状态机中的图表示，不过应该是简单易懂的，后面也会写一篇文章简单讲解下。从正则语言到 NFA 的过程是很容易理解的。我们来讲解正则中的三种基本操作（合并、连接、迭代）即可，因为这三种操作即可覆盖所有的正则表达式。

2

上图是简单易懂的，这是因为 ϵ−moves\epsilon-moves 的引入使得 NFA 存在一个输入可以执行多种状态转换的情况。因此能够看出当我们从入口出发，很轻松就可以看懂整个图，体现出其状态空间并不复杂。

NFA 到 DFA

这里我们首先要提到一个 ϵ−closure\epsilon-closure （也称为闭包）的定义。

ϵ−closure(s)\epsilon-closure(s): 从状态 ss 开始，通过 ϵ−moves\epsilon-moves 能到达的所有状态的集合（包括其自身）。 我们可以通过下述的例子进行理解。

3

根据定义我们可以获得：

  • ϵ−closure(B)={B,C,D}\epsilon-closure(B)=\lbrace B,C,D\rbrace:
  • ϵ−closure(G)={A,B,C,D,G,H,I}\epsilon-closure(G)=\lbrace A,B,C,D,G,H,I\rbrace
请注意!

对于 B 来说，除了自身，其次它可以通过 ϵ−moves\epsilon-moves 到达 C 和 D；对于 G 来说，除了自身，很明显它可以到达 H，A，接着进一步的延伸，H 可以到达 I，A 可以到达 B 进而到达 C、D。

在此基础上，我们便可以定义一个运算a(X)={y∣x∈X∧x→ay}a(X)=\lbrace y|x\in X\wedge x\stackrel{a}\rightarrow y\rbrace。 用于表示从一个集合状态 XX 经过输入 aa 后的得到的集合状态。

于是，就可以定义 NFA 到 DFA 的过程了，转换出的 DFA 应满足：

  • 状态集合：subsets of S,Ssubsets\ of\ S, S 代表 NFA 所有状态的集合。
  • 初始状态：ϵ−closure(s),s\epsilon-closure(s), s 代表 NFA 中的起始状态。
  • 终止状态：{X∣X∧F≠∅},F\lbrace X|X\wedge\mathcal{F}\ne\emptyset\rbrace, \mathcal{F}代表 NFA 中的终止状态集合。
  • 状态转换操作：X→aY if Y=ϵ−closure(a(X))X\stackrel{a}\rightarrow Y\ if\ Y=\epsilon-closure(a(X))

于是乎我们可以将上面的 NFA 转换为 DFA 如下：

4

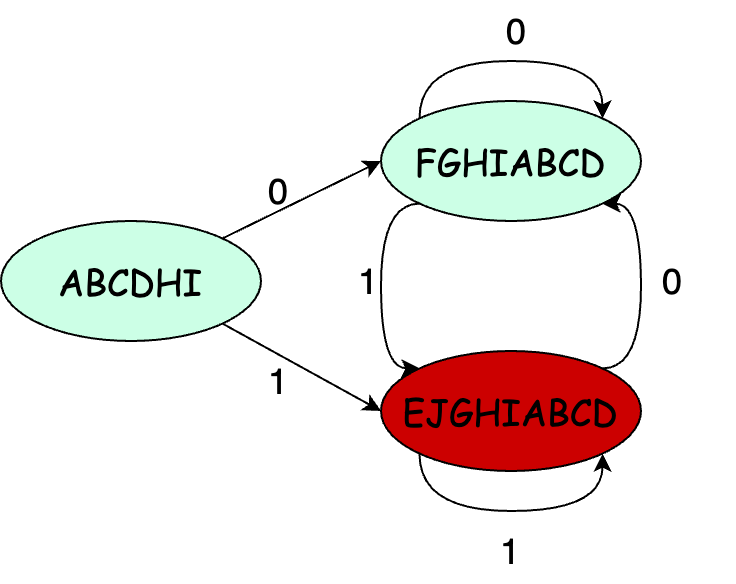
有图可见，DFA 中所有的状态转换路径都是唯一确定的，这使得 DFA 的执行速度通常将 比 NFA 快很多（也应证之前所说的优点）。然而，由于 DFA 的每个状态节点都是 NFA 状态集合的一个子集，这使得在大多情况下由 NFA 转换成为 DFA 会出现状态数量呈现指数级增长。另外，如果状态数量增长达到一定程度导致状态表超过主存容量时，DFA 真正的运行时间还会加上读取磁盘的时间，这将导致其执行时间成倍地增加。

因此，在现代有关词法分析的工具中，选择 NFA 还是 DFA 来模拟正则表达式是根据具体的使用场景来决定的。

如果是编译器中的词法分析器，显然使用 DFA 是更好的方式。因为其正则表达式基本固定，并且词法分析过程需要被频繁地调用。这种情况下将 NFA 转换成为 DFA 的开销是值得的。相比之下，对于另外的词法处理工具，例如 grep，由于需要用户指定不同的正则模式，其直接模拟 NFA 来执行将会是更好的选择。

动手实现词法分析

如果想要进一步研究词法分析在不同语言中的具体应用，这里有 flex©、JFlex(Java)、PLY(Python)。

参考文档及视频

Kaiyuan Blog

bilibili-斯坦福大学编译器

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

快来参与讨论吧~