Regular Language vs. Formal Language

Regular Language vs. Formal Language

正则语言（Regular Language） 是我们在讲词法分析时所提及的一个概念，它是可以用正则表达式或者自动机所描述的语言，常常用于解析和设计编程语言当中。正则语言和有限自动机可以对需要极少量内存的计算问题进行建模。如果有一个有限自动机可以识别一种语言，那么它就是一种正则语言。 除此之外，这里还有一个概念叫做形式语言（Formal Language），而正则语言就是其中的一种。

形式语言

首先对于一门人类语言，它本质上都是由字符组成的，在经过人类赋予了其特殊含义后从而拥有了语义。我们以英文为例，每个单词都是由 26 个英文字符定义的（这里可能不够严谨），如果出现了字母表以外的字符，那必然会造成不认识的情况，因此要想一门语言被完整理解，那么就必须规定其具有一个有限的、完整的字母表才可以。对于编程语言亦是如此。

语言的概念理解了之后，我们便来介绍什么是形式语言。形式语言的定义是用精确的数学或机器可处理的公式定义的语言。这也是我们想要 Compiler 或者说 Programming Language 完成的任务，即将人类理解的语言转为机器可以执行的语言，但不管高阶还是低阶语言，本质上就是语言和字符串的转换。

回到根本上，形式语言就是希望能够通过规则，让机器能够理解字符经过操作后所蕴含的含义。

本质：Alphabet --> Language /

In English: English characters --> English sentences

In C : ASCII --> C program

正则语言

正则语言作为形式语言的一种，它必然有着形式语言的一个特性，即都需要存在一个字母表（Alphabet）$\sum$，也就是一个该语言所有的字符集合。而这个集合往往是由空符号和其他字符构成（这里需要注意的是字母表一定是一个有限集合（finite set））。

正则语言在正则表达式在语言层面上的定义，主要由以下两部分组成：

• 基本单元
  • 单一字符集合。例如一个单一字符 'c'，它实际代表的是一个集合 {'c'} 。
  • 空字符 ϵ 。要注意它代表的是 {''}，而不是空集 {}。
• 基本操作：
  • 合并（Union）：$A+B=\lbrace a|a\in A\rbrace \cup\lbrace b|b\in B\rbrace$
  • 连接（Concatenation）：$AB=\lbrace ab|a\in A,b\in B\rbrace$
  • 迭代（Iteration）：$A^*=\cup_{i\ge 0}A^i$

Kleene 在 20 世纪 50 年代提出了上述三种基本运算符，Iteration 又可以记做 Kleene Star。

由上述定义可知，正则语言就是能够由字符表中的字符经过 3 种基本操作后表述语义的一种语言。我们举个例子来说，$1^*=\cup_{i\ge 0}1^i=11...1=All\ string\ of\ 1$，即它代表的是一个全由 1 构成的字符串，共 i 个字符。

一个小特点

Meaning Function L maps syntax to semantics.

形式语言中还有一个重要的概念叫做意义函数 L（Meaning Function），负责将句法映射到语义，而它有一个重要的特点就是多对一。如下图所示，一个字符串 000 可以由多种正则方法去表示，同样每个句法应该对应表示一个语义，然而每个语义却可以对应多个句法。

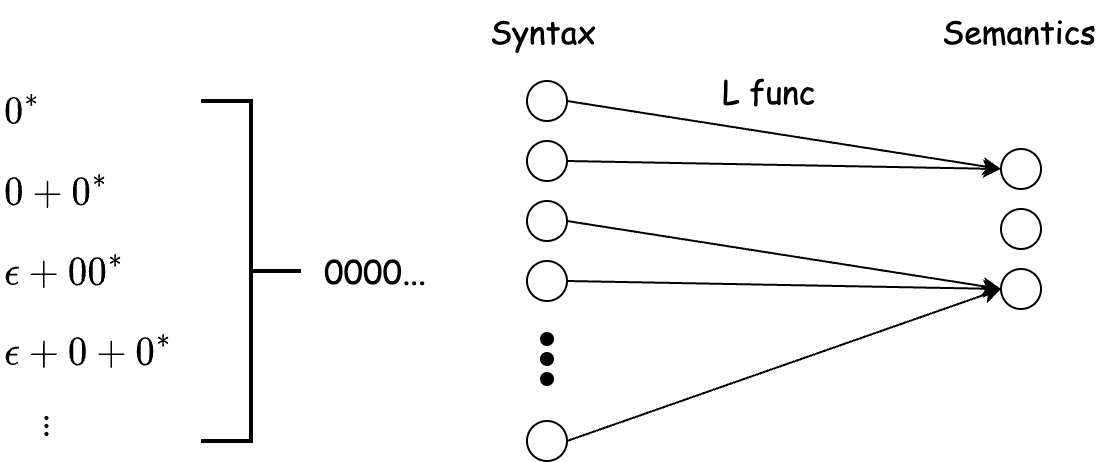
那为什么是多对一？答案是避免歧义！

当我们输入给机器时，我们希望的是机器能够做出一个我们希望的行为，而不会做出其他的事情，因此需要准确的表述，避免机器理解出现偏差。